Έστω ότι έχουμε μια οικονομία (την Ημεδαπή), η οποία παράγει δύο αγαθά τυρί (Qc) και κρασί (Qw) χρησιμοποιώντας έναν παραγωγικό συντελεστή, την εργασία (L). Η τεχνολογία παραγωγής, μπορεί να συνοψισθεί στην παραγωγικότητα της εργασίας στην παραγωγή κάθε προϊόντος (είναι ο μοναδικός παραγωγικός συντελεστής).
Αν:
aL c : η παραγωγικότητα της εργασίας στην παραγωγή τυριού (δηλαδή, πόση ποσότητα εργασίας απαιτείται στη χώρα Α για την παραγωγή μιας μονάδας τυριού).
aLw : η παραγωγικότητα της εργασίας στην παραγωγή κρασιού στη χώρα Α (δηλαδή, πόση ποσότητα εργασίας απαιτείται στη χώρα Α για την παραγωγή μιας μονάδας κρασιού).
Qc : η συνολικά παραγόμενη ποσότητα τυριού.
Qw : η συνολικά παραγόμενη ποσότητα κρασιού.
L : η συνολική ποσότητα εργασίας.
τότε η συνολική ποσότητα εργασίας κατανέμεται μεταξύ των δύο κλάδων σύμφωνα με την σχέση:
aLc ·Qc +aLw · Qw = ή < L (1)
Από την παραπάνω σχέση προκύπτει η καμπύλη παραγωγικών δυνατοτήτων της οικονομίας (που δείχνει πόση ποσότητα τους ενός προϊόντος μπορεί να παραχθεί για κάθε δεδομένη ποσότητα του άλλου):
aLc * Qc +aLw * Qw =L
Από τη σχέση αυτή μπορεί να εξαχθεί και το κόστος ευκαιρίας του τυριού ως προς το κρασί, σύμφωνα με το οποίο: για να παραχθεί μια μονάδα τυριού απαιτούνται aLc μονάδες εργασίας, οι οποίες θα στερηθούν από την παραγωγή κρασιού. Άρα το κόστος ευκαιρίας του τυριού ως προς το κρασί είναι aLc/aLw.
Σχήμα 1. Καμπύλη παραγωγικών δυνατοτήτων ημεδαπής
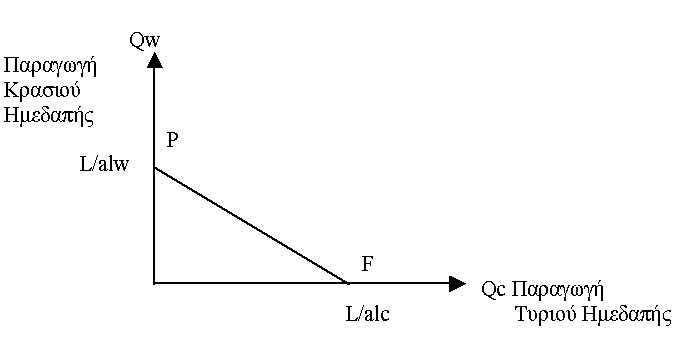
Ας υποθέσουμε ότι ο παραγωγικός συντελεστής εργασία εκφράζεται σε ώρες εργασίας και το πραγματικό ωρομίσθιο σε κάθε κλάδο παραγωγής θα είναι: Pc/aLc για τον κλάδο του τυριού και Pw/aLw για τον κλάδο του κρασιού. Αν ο κλάδος του τυριού προσφέρει υψηλότερο ωρομίσθιο από τον κλάδο του κρασιού (με αποτέλεσμα όλη η ποσότητα εργασίας να απασχολείται στον κλάδο του τυριού), τότε θα ισχύει:
Pc/aLc>Pw/aLw > Pc/Pw>aLc/aLw (2)
Δηλαδή, μια οικονομία (με τα χαρακτηριστικά του υποδείγματός μας), θα εξειδικευτεί στην παραγωγή ενός προϊόντος Χ, αν η σχετική τιμή του ως προς το άλλο προϊόν Ψ υπερβαίνει το κόστος ευκαιρίας του Χ ως προς το Ψ.